27
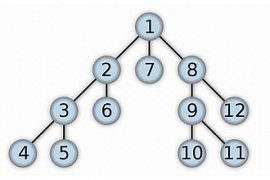
Depth First Search
In graph theory, etc. search, depth first (briefly DFS) is an algorithm scrolling graph that for scrolling or searching a tree or a graph goes to work.
search Strategy Depth-First, for scrolling the graph, as the name suggests, the \"search deeper in the graph, until possible\".
algorithm from the root starts (in the graph or tree without a root Vertex enviable as Root, choose to be) and in each step the neighbors of the vertices of the current through the ridge, the outgoing head of the current, respectively, and, as soon as the confrontation with the neighbor that had previously not seen. recursively, for which the helm as the head of the current runs. In the event that all the neighbors had previously been seen. the algorithm back round and makes the implementation of the algorithm for from which to helm the ongoing've reached, etc. continues. In other words, the algorithm as much as possible, to a depth of more and more and goes in the face of a deadlock rollback. This process, as long as all vertices, attainable from the root are seen continues.
Also in the issues that different states correspond to the vertices of a graph have, and problem solving requires finding the top of the goal with the peculiarities of the certain. search depth-first for acts. So that each time the algorithm to the first neighbor of a vertex in the Graph Search and in the result each time to a depth of more and more in the graph goes up to reach that all its neighbors have been seen that in the recent state of the ... algorithm to the first back that the neighbor is still not seen. This trend, to the point continues that the head goal is found, or probably all, the graph scrolling. Of course, the implementation of a clever algorithm with the choice of arrange the right to check the neighbors haven't seen the helm of the current to if the first algorithm to check the neighbor pay that for topical and selective guzzle to the helm of the goal closer. will be possible which usually in reducing the time to run effective.
from a practical point of view, for the implementation of the algorithm, a stack (stack) is used. So that each time the login to a head not seen, then the vertices in the Stack put and when back round the top of the stack, we remove. So during the whole algorithm, the first element of the stack top are check. Implementation details continue will come.
When in the graph, a portion of the search that makes it possible to save full them due to the memory limit does not exist, in the event that during the path traversal by an algorithm that from the roots start. very big. the algorithm the problem will be encountered. In fact, this is a simple solution that \" that up to now we've seen the save, We\" does not always work. As possible enough memory to do this, we don't have. Of course, this problem by limiting the depth of search in each time implementation of the algorithm can be solved that eventually the algorithm, the deepening of repetitive (Iterative Deepening) will last....
search Strategy Depth-First, for scrolling the graph, as the name suggests, the \"search deeper in the graph, until possible\".
algorithm from the root starts (in the graph or tree without a root Vertex enviable as Root, choose to be) and in each step the neighbors of the vertices of the current through the ridge, the outgoing head of the current, respectively, and, as soon as the confrontation with the neighbor that had previously not seen. recursively, for which the helm as the head of the current runs. In the event that all the neighbors had previously been seen. the algorithm back round and makes the implementation of the algorithm for from which to helm the ongoing've reached, etc. continues. In other words, the algorithm as much as possible, to a depth of more and more and goes in the face of a deadlock rollback. This process, as long as all vertices, attainable from the root are seen continues.
Also in the issues that different states correspond to the vertices of a graph have, and problem solving requires finding the top of the goal with the peculiarities of the certain. search depth-first for acts. So that each time the algorithm to the first neighbor of a vertex in the Graph Search and in the result each time to a depth of more and more in the graph goes up to reach that all its neighbors have been seen that in the recent state of the ... algorithm to the first back that the neighbor is still not seen. This trend, to the point continues that the head goal is found, or probably all, the graph scrolling. Of course, the implementation of a clever algorithm with the choice of arrange the right to check the neighbors haven't seen the helm of the current to if the first algorithm to check the neighbor pay that for topical and selective guzzle to the helm of the goal closer. will be possible which usually in reducing the time to run effective.
from a practical point of view, for the implementation of the algorithm, a stack (stack) is used. So that each time the login to a head not seen, then the vertices in the Stack put and when back round the top of the stack, we remove. So during the whole algorithm, the first element of the stack top are check. Implementation details continue will come.
When in the graph, a portion of the search that makes it possible to save full them due to the memory limit does not exist, in the event that during the path traversal by an algorithm that from the roots start. very big. the algorithm the problem will be encountered. In fact, this is a simple solution that \" that up to now we've seen the save, We\" does not always work. As possible enough memory to do this, we don't have. Of course, this problem by limiting the depth of search in each time implementation of the algorithm can be solved that eventually the algorithm, the deepening of repetitive (Iterative Deepening) will last....