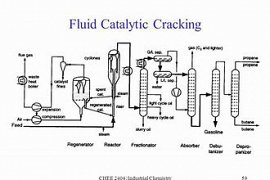
34
Non deterministic Polynomial
In theory, the complexity of computing NP is one of the most fundamental classes. NP stands for “non deterministic polynomial”, which is the current implementation it refers.
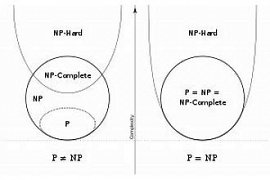
NP set all issues, decisions that find the answer, yes, for they include the simple proof that the answer really should be yes. Generally, the more accurate the proof simple Should to be investigated at a time, run a few sentences in a Turing machine algebras. In contrast to this definition, NP set, issues a decision, which is called a run time polynomial in a Turing machine, non-algebraic evaluation. Class complexity P one of the members of NP, but NP contains the class, another important as well. That is the most complex, they are NP-Complete is as to them no algorithm known runs in time polynomial does not exist .
the most important question that now, for the classes in this theory is whether P=NP a? This question asks whether such an algorithm really matters, NP-Complete and total NP there or not. This widespread belief out there that this equality can not be true....
NP set all issues, decisions that find the answer, yes, for they include the simple proof that the answer really should be yes. Generally, the more accurate the proof simple Should to be investigated at a time, run a few sentences in a Turing machine algebras. In contrast to this definition, NP set, issues a decision, which is called a run time polynomial in a Turing machine, non-algebraic evaluation. Class complexity P one of the members of NP, but NP contains the class, another important as well. That is the most complex, they are NP-Complete is as to them no algorithm known runs in time polynomial does not exist .
the most important question that now, for the classes in this theory is whether P=NP a? This question asks whether such an algorithm really matters, NP-Complete and total NP there or not. This widespread belief out there that this equality can not be true....